The Lambda Calculus
Abstract
This post is part of a series on how to reason about our code. In particular, it describes the λ Calclus, a precursor to the formal language understood by Coq, an interactive proof assistant with which I am learning to work. More background can be found here.
This post may seem pedantic, or at least far afield from reasoning about our code. However, at the end of the day, Coq is a system for writing down valid terms in a certain formal language, and to understand that language I wanted to go back to the start: Church's λ Calculus.
The Context
Our story begins roughly one hundred years ago. Mathematicians at the time were quite interested in what, precisely, was meant by computation. Of course, we all have an intuitive notion of that that means; people have been writing-down algorithms since the time of the ancient Greeks, if not further; the word "algorithm" itself is an Anglicization of the name of the ninth century Persian mathematician al-Kwārizmī, but by "precisely" we mean "in a form which we can use to prove things".
It was all due to the "Hilbert Program"– David Hilbert's search for a way to formalize all of mathematics. He envisioned a machine (whether abstract or concrete, I'm not sure) to which one could hand mathematical statements written down in some sort of domain-specific language, and from which one would receive an answer: "true" or "false". Of course, Gödel's Incompleteness Theorems put the Hilbert Program out of business, but that's a different story.
Our story concerns how, exactly, such a machine might work. In order to prove things like Gödel's Incompleteness Theorems, mathematicians needed a rigorous way in which to talk about computation. In a very short period, in the nineteen thirties, three models for computation emerged:
- Kurt Gödel proposed the Theory of Recursive Functions
- Alan Turing proposed the model of the Turing Machine
- and Alonzo Church proposed the λ Calculus
The three were quickly shown to be equivalent in that anything that we could compute in one system could also be computed in the other two. That said, it is the last with which we are concerned. Despite dating back a century, people continue to study the λ Calculus today. In fact, the use of the word "lambda" to describe an anonymous function whipped-up on the spot & then thrown away after use in industrial languages like Java, C++, Rust & so forth, harkens back to the λ Calculus.
So What Is It?
Start with a set of variables \(\mathscr{V}=\{a,b,c...\}\). The set \(\mathscr{V}\) is infinite, but we'll begin with the lower-case Latin letters. Then the λ Calculus is the set of terms formed according to the following three rules:
- naming :: if \(x\in \mathscr{V}\), then \(x\) is a term (in the λ Calculus)
- abstraction :: if \(T\) is a term & \(x\in \mathscr{V}\), then \(\lambda x.T\) is a term, where \(x\) may (or may not) occur in \(T\)
- application :: if \(T_1\) and \(T_2\) are terms, then \(T_1 \enspace T_2\) is a term
Using these rules, we can build-up an infinite set of terms, for instance:
\begin{align} &x\nonumber\\ &y\nonumber\\ &\lambda x.x \nonumber\\ &\lambda x.\lambda y.x \nonumber\\ &\lambda x.\lambda y.y \nonumber\\ &\lambda x.\lambda y.\lambda z.((z \enspace x) \enspace y) \nonumber\\ &\ldots \end{align}Beyond syntax, the three grammar rules correspond to operations that will be familiar to the programmer, the functional programmer in particular:
- naming represents the act of giving a name to quantity in a program
- abstraction represents the act of taking a given computation and turning it into a resuable function with a formal parameter
- application represents the act of applying an actual parameter to an abstraction
How Do We Compute in the λ Calculus?
I've made some bold claims; how can such a simple set of rules for writing down terms be a model for general computation? Well, for starters, the last four examples in (1) above can be considered examples of the functions identity, select-first, select-second & make-pair, respectively. To see this, we need to consider computation in the λ Calculus.
Application & Term Rewriting
The engine for computation in the λ Calculus is rule three, application. In particular, when \(T_1\) is an abstraction, we are allowed to re-write applications by substituting \(T_2\) for \(x\) throughout \(T_1\).
For example, consider the application \(\lambda x.x \enspace y\). We rewrite this by substituting \(y\) for \(x\) in the abstraction \(\lambda x.x\). The body of the abstraction is just \(x\), yielding \(y\):

Figure 1: Term rewriting
Imagine that the \(x\) is a formal parameter and we're invoking the function \(\lambda x.x\) with an actual parameter \(y\). More generally, we see that the abstraction \(\lambda x.x\) is the identity function.
Let's consider a second example: \((\lambda x.\lambda y.x \enspace a) \enspace b\). This is two applications:
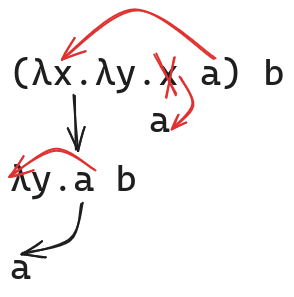
Figure 2: Selecting the first parameter
Notice in the second case, the formal parameter \(y\) appeared nowhere in the body of the abstraction, so we simply return the body unchanged. Expressed more succinctly:
\begin{align} &(\lambda x.\lambda y.x \enspace a) \enspace b &\rightarrow \nonumber\\ &\lambda y.a \enspace b &\rightarrow \nonumber\\ a \end{align}We see a few other things, here. Firstly, this is how the λ Calculus handles functions of more than one variable: successive application. Another way to view it is that \(\lambda x.\lambda y.T\) is a function of a single variable \(x\) that returns a function of a single variable \(y\). Regarding functions of multiple variables as successive functions of single variables is called "Currying", after the logican Haskell Curry (who lent his name to the Haskell programming language, but again, that's another story).
Secondly, we also see that the term \(\lambda x.\lambda y.x\) when applied to two variables, returns the first. Call this select-first. I'll let the reader convince themselves that select-second := \(\lambda x.\lambda y.y\) will select the second parameter.
As a third example, let's consider the term \(\lambda x.\lambda y.\lambda z.((z \enspace x) \enspace y)\). Let's apply this to the variable \(a\):
\begin{align} &\lambda x.\lambda y.\lambda z.((z \enspace x) \enspace y) \enspace a&\rightarrow \nonumber\\ &\lambda y.\lambda z.((z \enspace a) \enspace y) \nonumber \end{align}Let's apply that result to \(b\):
\begin{align} &\lambda y.\lambda z.((z \enspace a) \enspace y) \enspace b &\rightarrow \nonumber\\ &\lambda z.((z \enspace a) \enspace b) \nonumber \end{align}
So, we started with \(a\) & \(b\) and we wound up with a term taking a single parameter that is seemingly expected to be an abstraction (since we apply it). Let's feed that function select-first:
In other words, applying the term \(\lambda x.\lambda y.\lambda z.((z \enspace x) \enspace y)\) to two parameters yields a term that "encodes" the two parameters into itself. That term can be applied to abstractions that will perform various operations on the two terms. For instance, applying it to select-first will, well, select the first parameter (and likewise select-second). In this way, we can regard the term \(\lambda x.\lambda y.\lambda z.((z \enspace x) \enspace y)\) as make-pair.
Finally, note that application is left-associative, so that L M N is (L M) N, and application takes precedence over abstraction, so \(\lambda x.M \enspace N\equiv\lambda x.(M \enspace N)\). Finally, Currying is understood, so we may write \(\lambda xyz\ldots\) for \(\lambda x.\lambda y.\lambda z.\ldots\).
Free & Bound Variables; Alpha Equivalence
The reader may by now have noted a potential problem: what if we applied to a variable \(x\) an abstraction that contains other abstractions that also use the variable \(x\)? For instance, consider the following application:
\begin{equation} \lambda x.(x \enspace \lambda x.x) \enspace y \end{equation}We can't just overwrite \(x\) with \(y\) blindly; intuitively, the "x" in the subterm \(\lambda x.x\) is a different "x" than the "outer" "x" appearing in \(\lambda x.(x \enspace\ldots\).
This leads us to the notion of "free" & "bound" variables in the λ Calculus. Actually, there are three categories of variable occurrences in any term: binding, bound & free. Binding occurrences are simply when a variable appears immediately after the λ in an abstraction. Intuitively, "bound" occurrences are occurrences of a variable in a term that correspond to a binding occurrence. The "free" occurrences are everything else.
More precisely, we build-up the definitions like so:
- if \(x\in \mathscr{V}\) then the variable \(x\) occurs freely in term \(x\)
- if \(M N\) is a term, then all variables occurring freely in \(M\) & \(N\) are still free in the term \(M N\)
- if \(\lambda x.M\) is a term, then the \(x\) on the left of the '.' is a binding occurrence, and all free occurrences of \(x\) in \(M\) become bound. Bound occurrences of \(x\) remain bound, and free occurrences of other variables remain free.
To continue our example (4), the "inner" occurrence of \(x\) is bound in \(\lambda x.x\) and the "outer" occurrence is bound in \(\lambda x.(x \enspace \ldots\).
Another way to look at this is to envision terms as a tree structure in which application and abstraction are nodes:
- if \(x\in \mathscr{V}\) then the term \(x\) is a tree with a single leaf node labeled \(x\)
- if \(M\) & \(N\) are terms, then we visualize \(M \enspace N\) as a tree whose root is labelled "appl" and whose two children are the trees representing \(M\) & \(N\)
- if \(M\) is a term, then we visualize the term \(\lambda x.M\) as a tree whose root is labelled "abst \(x\)" and whose single child is the tree representing \(M\)
For instance, the tree representation of \(\lambda x.(x \enspace \lambda x.x) \enspace y\) would be:

Figure 3: Tree representation of \(\lambda x.(x \enspace \lambda x.x) \enspace y\)
We can see whether a given variable occurrence is bound by following the path from the corresponding leaf node to the root and observing whether the path passes through a node labelled "abst" with that variable name. In this case, both occurrences of \(x\) are bound (albeit by different abstractions), while \(y\) is free.
The free variables of a term \(T\), denoted \(FV(T)\), are defined as follows:
- if \(x\in \mathscr{V}\), then \(FV(x)=\{x\}\)
- \(FV(M \enspace N) = FV(M)\cup FV(N)\)
- \(FV(\lambda x.M) = FV(M)\setminus\{x\}\)
For example:
\begin{align} &FV(\lambda x.z \enspace x) &= \nonumber\\ &FV(z \enspace x) \setminus \{x\} &= \nonumber\\ &(FV(z) \cup FV(x)) \setminus \{x\} &= \nonumber\\ &(\{z\} \cup \{x\}) \setminus \{x\} &= \nonumber\\ &\{z, x\} \setminus \{x\} &= \nonumber\\ &\{z\} \end{align}and
\begin{align} &FV(\lambda x.(z \enspace x) \enspace x) &= \nonumber\\ &FV(\lambda x.z \enspace x) \cup FV(x) &= \nonumber\\ &(FV(z \enspace x) \setminus \{x\}) \cup \{x\} &= \nonumber\\ &((\{z\} \cup \{x\}) \setminus \{x\}) \cup \{x\} &= \nonumber\\ &(\{z, x\} \setminus \{x\}) \cup \{x\} &= \nonumber\\ &(\{z\} \cup \{x\}) = \{z, x\} \end{align}Nb that \(FV(T)\) returns the set of variables that occur free anywhere in \(T\); variables therein may also occur bound.
The intuition here is that bound variables are "placeholders" that can be re-named at will without changing the essential meaning of a term. For instance, \(\lambda y.y\) expresses the identity function just as well as \(\lambda x.x\), but \(\lambda y.a \enspace y\) is fundamentally different than \(\lambda y.b \enspace y\).
We can formalize this via the operation of renaming a binding variable. Denote by \(M^{x\rightarrow y}\) the result of replacing every free occurrence of \(x\) in \(M\) with \(y\). If \(y\not\in FV(M)\), and \(y\) is not a binding variable in \(M\), then we say \(\lambda x.M =_{\alpha} \lambda y.M^{x\rightarrow y}\).
We require the first condition (\(y\not\in FV(M))\) because if there were a free occurrence of \(y\) already somewhere in \(M\), that occurrence would inadvertently become bound by the renaming. For instance, consider \(\lambda x.x \enspace y\). If we tried to rename \(x\) to \(y\) here, we would wind-up with \(\lambda y.y \enspace y\), which is not at all the same.
The second condition is required for similar reasons: if the variable to which we are rewriting is in use as a binding variable, the rewrite operation could change the structure of the term. For instance, imagine \(\lambda x.\lambda y.x\)– the \(x\) is bound by the first abstraction. Rewriting \(x\) to \(y\) would change it to being bound by the second.
Renaming the binding variable used by an abstraction is known as α-conversion, and two abstractions that differ by α-conversion are said to be α-equivalent. α-equivalence is a true equivalence relation on λ abstractions:
- \(\forall M, M =_{\alpha} M\)
- if \(M =_{\alpha} N\), then \(N =_{\alpha} M\)
- if \(L =_{\alpha} M\), and \(M =_{\alpha} N\), then \(L =_{\alpha} N\)
Furthermore, if \(M =_{\alpha} N\), then \(\forall L, M \enspace L =_{\alpha} N \enspace L\), and \(L \enspace M =_{\alpha} L \enspace N\).
Let's go back to the example that started this section (4) above. Since the body of the abstraction is itself an application, we can pick an α-equivalent version of \(\lambda x.x\), using some other variable that doesn't occur in this term, say \(q\). We can then rewrite the expression unambiguously & evaluate to something structurally equivalent as:
\begin{align} &\lambda x.(x \enspace \lambda q.q) \enspace y &\rightarrow \nonumber\\ &y \enspace \lambda q.q \end{align}Beta Reduction
Ever since "Application & Term Rewriting" above, we've been informally substituting actual parameters for formal in applications. Let's make that precise, following the exposition in "Type Theory & Formal Proof", sec. 1.6.
- if \(x\in \mathscr{V}\), then \(x[x:=N]\equiv N\)
- if \(y\in \mathscr{V}\), then \(y[x:=N]\equiv y\), if \(y\neq x\)
- \((P \enspace Q)[x:=N]\equiv (P[x:=N] \enspace Q[x:=N])\)
- \((\lambda y.P)[x:=N]\equiv \lambda z.(P^{y\rightarrow z}[x:=N])\), if \(\lambda z.P^{y\rightarrow z}\) is α-equivalent to \(\lambda y.P\) with \(z\not\in FV(N)\)
Let's work-out a few examples. \(x[x:=y \enspace z]\equiv y \enspace z\) should be clear: we're just rewriting \(x\) with \(y \enspace z\). Similarly, \(x[y:=a \enspace b \enspace c]\equiv x\), since the term we're rewriting doesn't occur in the rewrite target.
Let's consider \(((a \enspace b) \enspace (a \enspace c))[a:=x]\). This is also straightforward: push the substitution inside the application and rewrite \(a\) as \(x\): \((x \enspace b) \enspace (x \enspace c)\), which is clearly α-equivalent.
The last rule is the tricky one, again due to the tendency of changing which variables are bound to change the structure of the term in ways we probably don't want. Here, we need to pick a variable that is not free in \(N\), rename the binding variable in our abstraction (to use that variable), and only then carry-out the substitution. This is important because the variable \(y\) is the binding variable in the abstraction; if it occurred free in \(N\), we would change the term to something not α-equivalent (i.e. it would have a different structure). To see this, consider the following substitution: \((\lambda y.y \enspace x)[x:=x \enspace y]\). Let's suppose we ignore that step in the substitution & just proceed naively:
\begin{align} &(\lambda y.y \enspace x)[x:=x \enspace y] &\rightarrow \nonumber\\ &\lambda y.y \enspace (x \enspace y) \end{align}This yields something clearly wrong; applying the result to some other term will bind both the initial \(y\) and the \(y\) that now appears in what used to be a free variable.
The correct approach is to first pick a variable that does not occur free in the replacement, say \(z\), and rename the abstraction before the substitution:
\begin{align} &(\lambda y.y \enspace x)[x:=x \enspace y] &\equiv \nonumber\\ &(\lambda z.z \enspace x)[x:=x \enspace y] &\rightarrow \nonumber\\ &\lambda z.z (x \enspace y) \end{align}This allows us to define one-step β-reduction, denoted \(\rightarrow_{\beta}\): \((\lambda x.M) \enspace N\rightarrow_{\beta} M[x:=N]\). The subterm on the left-hand side (i.e. \((\lambda x.M) \enspace N)\) is called a redex (from "reducible expression") and the result a contractum.
Let's work an illuminating example (this is example 1.8.2 in "Type Theory & Formal Proof"). Consider the term \((\lambda x.(\lambda y.yx)z) \enspace v\). We see that we have two redexes available to us: the full term which is an application, and the sub-term \(\lambda y.yx\) applied to \(z\).
If we choose to perform one step of β-reduction on the full term, we get:
\begin{align} &(\lambda x.(\lambda y.yx)z)v &\rightarrow_{\beta} \nonumber\\ &(\lambda y.yv)z \end{align}and if we choose to do the same on the sub-term, we get:
\begin{align} &(\lambda x.(\lambda y.yx)z)v &\rightarrow_{\beta} \nonumber\\ &(\lambda x.zx)v \end{align}Note the terms are not the same, and they are not even α-equivalent (there's no way to just rename binding variables to make the syntactically the same). However, observe what happens if we perform one more β-reduction on each:
\begin{align} &(\lambda x.(\lambda y.yx)z)v &\rightarrow_{\beta} \nonumber\\ &(\lambda y.yv)z &\rightarrow_{\beta} \nonumber\\ &zv \end{align}and
\begin{align} &(\lambda x.(\lambda y.yx)z)v &\rightarrow_{\beta} \nonumber\\ &(\lambda x.zx)v &\rightarrow_{\beta} \nonumber\\ zv \end{align}It is not always the case that if we just apply β-reduction steps enough, we'll always "reduce down" to the same result, but in this case it is.
With this, we define β-reduction, denoted \(\twoheadrightarrow_{\beta}\): \(M\twoheadrightarrow_{\beta} N\) if there is an \(n\ge 0\) and terms \(M_0\) to \(M_n\) such that \(M_0\equiv M_n\), \(M_n\equiv N\) and for all \(i, 0\le i < n, M_i\rightarrow_{\beta} M_{i+1}\).
We say that \(M =_{\beta} N\), or that \(M\) & \(N\) are β-convertible or β-equal if there is a chain of \(M_i\), \(M_0\equiv M\), \(M_n\equiv N\), \(i \le 0 < n\) such that for each \(i\), we have either \(M_i\twoheadrightarrow M_{i+1}\) or \(M_{i+1}\twoheadrightarrow M_i\). The last condition may seem odd, but it's necessary to group all four terms shown in (10) through (13) into a single equivalence class.
Strong & Weak Normalization in the Lambda Calculus
Alright– at this point, we know how to "compute" in the λ Calclus: β-reduction. The reader may wonder, what does it mean for β-reduction to be "done"? Will β-reduction always halt? Do all terms behave as nicely as our example (10)?
We say that a term \(M\) is in β-normal form (β-nf) if \(M\) contains no redex; i.e. if there is no way to perform β-reduction to "reduce" it to a simpler form. We say that a term \(M\) has a normal form, or is β-normalizing, if there is an \(N\) in β-normal form such that \(M =_{\beta} N\). We say that such an \(N\) is a β-normal form of \(M\).
Intuitively, the β-normal forms of a term \(M\) are in some sense the "result" produced by evaluating \(M\). Continuing the example we started in (10), we see that \(zv\) is a β-normal form of \((\lambda x.(\lambda y.yx)z)v\).
Let's consider a few other examples, all once again from "Type Theory and Formal Proof". \(\lambda x.x \enspace x\) is known as the "self-application function". Let's apply it to itself:
\begin{align} &(\lambda x.x \enspace x) (\lambda x.x \enspace x) &\rightarrow_{\beta} \nonumber\\ &(\lambda x.x \enspace x) (\lambda x.x \enspace x) &\rightarrow_{\beta} \nonumber\\ &(\lambda x.x \enspace x) (\lambda x.x \enspace x) &\rightarrow_{\beta} \nonumber\\ \ldots \end{align}So the term \((\lambda x.x \enspace x) (\lambda x.x \enspace x)\) is not in normal form (it contains a redex) and it has no normal form, since β-reduction never terminates.
Define Ω to be this term. Then \((\lambda u.v)\Omega\) has two redexes: the full term and Ω. If we choose to reduce the full term, we get \(v\), which is in β-nf. If we choose the second, and keep doing so, we never terminate. So the choice of redex at each step is also important.
Inspired by these examples, we define strong- & weak-normalization. We say that a term \(M\) is weakly normalizing if there is an \(N\) in β-normal form such that \(M\twoheadrightarrow_{\beta} N\). We say \(M\) is strongly normalizing if there are no infinite reduction paths starting from \(M\).
The Church-Rosser theorem states that if, for a given term \(M\), we have \(M\twoheadrightarrow_{\beta}N_1\) and \(M\twoheadrightarrow_{\beta}N_2\), then there is a term \(N_3\) such that \(N_1\twoheadrightarrow_{\beta}N_3\) and \(N_2\twoheadrightarrow_{\beta}N_3\). IOW, we can at least rest easy that if a computation has an outcome, it is independent of the order in which the reductions are performed.
Where Are We?
The λ Calculus is a general model for computation; in fact, it's Turing Complete, although we haven't gone into that here. In fact, it's so general, one can write programs that never terminate. Church sought to address that by adding types to the λ Calclus, and that will be the topic of my next post.
In the meantime, you can find Church's original paper here. For an extremely approachable introduction to the λ Calculus, I recommend "An Introduction to Functional Programming through Lambda Calculus" by Greg Michaelson. That's where I got the example functions select-first, select-second & make-pair.
I've also relied heavily on "Type Theory and Formal Proof: An Introduction", by Nederpelt & Guevers, for examples in this post, but also for my understanding generally. It's a very nice exposition of Type Theory starting from zero, and I was clued-in to it by a video series entitled The Lambda Cube Unboxed.
05/14/24 17:56