A Concrete Example of Symbolic Execution
Introduction
In my last post, I argued that testing is a poor substitute for reasoning about our code, and provided a crude illustration of what I meant by "reason about". In this post I'm going to explore one way in which we can reason about code more deeply & show a real-world example.
Symbolic Execution– Preamble
When I was a young(er), I would sometimes sit with a paper & pencil and "work through" some code I had written, either to be sure it worked, or to figure out why it wasn't (this was 6502 assembly on an Apple II+– no symbolic debuggers!) Each variable got a line, and as I walked through my code manually, I'd scratch through the old & write down the new value for each variable as it changed. So, for instance, thinking about a function like this:
int highly_contrived(int *A, int nA, int x, int y) { if (x + 2*y > 3) { // 1 ++x; // 2 y = x/2; // 3 return A[3*x - 2*y]; // 4 } else { --x; // 5 y += x; // 6 return A[y + 2*x]; // 7 } }
would lead to something like this:
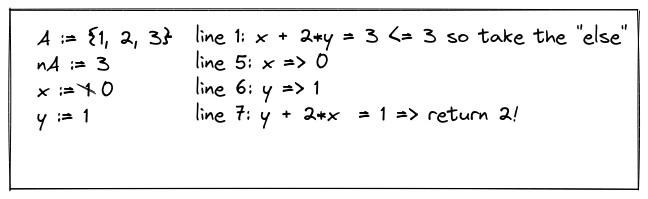
We can see that for \(A = [1, 2, 3], nA = 3, x = y = 1\), this function returns \(\mathcal{A}[1] = 2\)– all well & good.
We might imagine input values for which the array indicies could be out-of-bounds…

but what if we can't imagine input values that make our code fail? This approach works when I've got a specific set of inputs in which I'm interested & I want to see what my code does when I hand it those particular inputs. It doesn't answer questions like "do there exist any inputs for which the array indices will be out of bounds?"
There's a different approach we can take: imagine going through this exercise, but instead of assigning values like "11", or "-17" to our variables, we're going to write down things we know about them:
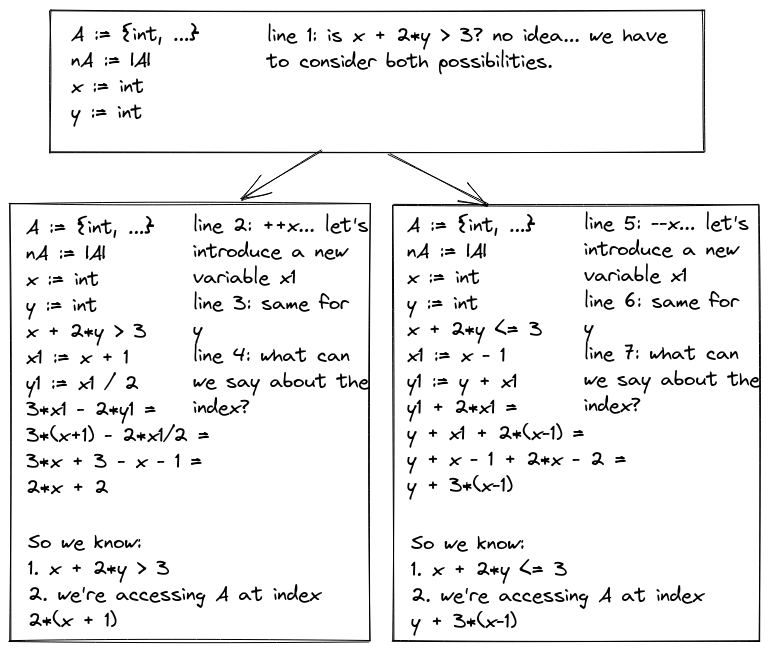
Cool. So now we can characterize our array indicies in terms of our inputs:
- if \(x + 2y > 3\), then we're accessing \(\mathcal{A}\) at index \(2(x+1)\)
- if \(x + 2y <= 3\), then we're accessing \(\mathcal{A}\) at index \(y + 3(x-1)\)
Now we can say precisely what we're looking for in our inputs: are there any \(x\), \(y\), and \(\mathcal{A}\) such that:
- \(x + 2y > 3\) and either \(2(x+1) < 0\) or \(2(x+1) >= |\mathcal{A}|\)
- or, \(x + 2y <= 3\) and either \(y + 3(x-1) < 0\) or \(y + 3(x-1) >= |\mathcal{A}|\)
In other words, are there any \(x, y, \mathcal{A}\) that will make our array index operations be out of bounds?
Satisfiability Modulo Theories
What if we had an oracle of which we could ask questions like: are there any \(x, y, |\mathcal{A}|\) such that:
\begin{equation} x + 2y > 3 \land (0 > 2(x+1) \lor |\mathcal{A}| <= 2(x+1)) \end{equation}If we had such a thing (and could code to it), then we would be reasoning about our code. If no such values exist, we know our code is sound in a way beyond being unable to come up with negative test cases. If there are such values, then the oracle has handed us a negative test on a silver platter.
Well, there are such oracles, we can program to them & they're called "SMT Solvers". This is going to be a whirlwind introduction to them, but I hope to write more deeply on them later. In the meantime, you can read Dennis Yurichev's very accessible SAT/SMT by Example or the Z3 paper.
"SMT" stands for "Satisfiability Modulo Theories". "Satisfiability" refers to a well-known NP-complete problem: boolean satisfiabilty, or just "SAT" for short. The problem is deceptively simple. Given a set of boolean variables \(x_i, i=1,...n\) determine whether there is any assignment to those variables such that the equation
\begin{equation} (X_1 \lor X_2 \lor X_3...) \land ... \end{equation}where each \(X_i\) is either \(x_j\) or \(\lnot x_j\) for some \(j\). Given an assignment to the \(x_i\), checking whether that assignment satisfies the given formula is trivial. But finding an assignment that satisfies the formula… well, that takes some doing. The problem is an exemplar of the reason so many researches suspect that \(P \neq NP\): it is an NP-complete problem that has been subjected to exhaustive study: if \(P\) were equal to \(NP\), surely this problem (or some other NP-complete problem) would have fallen by now, given the collective brain-power devoted to solving it. Regardless, while the worst-case performance of every known algorithm is exponential, when it comes to real-world problems we'd like to solve, it turns out we can do quite a bit better than that.
SMT builds upon SAT to extend the domain of statements about which we can reason beyond boolean variables to propositional logic: asking whether there are assignments that can satisfy statements containing not just boolean variables (and their negations), but propositions involving variables over other domains. What domains? Things like the integers or bit vectors. What propositions? Things like "greater than", or "is a power of 2".
One such SMT solver is Z3; let's ask Z3 about our array index operations:
(declare-const x Int)
(declare-const y Int)
(declare-const nA Int)
(assert (> (+ x (* 2 y)) 3))
(assert (or (< 0 (* 2 (+ x 1)))
(>= (* 2 (+ x 1)) nA)))
(check-sat)
(get-model)
This is a little program in smt-lib. We begin by declaring three variables \(x\), \(y\), & \(nA\). Let's then check our first branch: we assert that \(x + 2y > 3\) and then assert that the resulting array index is out-of-bounds by either being less than zero or greater than the largest index. Finally, we ask Z3 to check whether our conditions are satisfiable and, if so, to give us an example.
z3 -smt2 first.smt2
sat
(
(define-fun x () Int
0)
(define-fun y () Int
2)
(define-fun nA () Int
0)
)
It turns out that it is: if \(x = 0\), \(y = 2\), and \(nA = 0\) then \(x + 2y = 4 > 3\) so we take the "if branch". \(x :=> 1\), \(y := 0\), \(3x - 2y = 3 \geq nA\).
But that's kind of dumb… let's constrain \(|\mathcal{A}| > 0\).
(declare-const x Int)
(declare-const y Int)
(declare-const nA Int)
(assert (> nA 0))
(assert (> (+ x (* 2 y)) 3))
(assert (or (< 0 (* 2 (+ x 1)))
(>= (* 2 (+ x 1)) nA)))
(check-sat)
(get-model)
Well, that turns out to be trivial to satisfy, as well:
z3 -smt2 first.smt2
sat
(
(define-fun nA () Int
1)
(define-fun x () Int
0)
(define-fun y () Int
2)
)
Alas, it seems that our highly contrived function is not salvagable.
Symbolic Execution – Practice
This is all very interesting, but can it be made into a practical tool for reasoning about code? Perhaps it can. The idea of coding up the process of my crude illustration of "working through" your code, writing down what is known as you go, and then asking questions of an SMT solver at interesting points has been implemented. In fact there are many such "symbolic exection engines" out there.
One of the better-known is klee. Klee is a symbolic execution engine that operates on LLVM bitcode. LLVM is a toolkit for building compilers. Clang is based on it, as is rustc. You can ask LLVM to compile your code to an intermediate representation called "bitcode". Think of klee as an interpreter for LLVM bitcode. klee will begin "executing" your program, keeping track of variable values if those variables are "concrete" and noting down things we know about their values if they are "symbolic". At branch points (like an if-then-else statement), klee will use an SMT solver to see if both branches are feasible– that is, are there any inputs for which each branch might be taken? If so, klee "forks" your process. Not literally, in the Linux sense of hte word, but in terms of its interpretation: it will create a copy of the program's state for each branch, add the condition that jumps to the "if" branch to what is known about that copy, and the same, mutatis mutundis for the "else" branch.
Symbolic execution engines generally have to address two problems:
- the "path explosion" problem: in any non-trivial program, the number of paths through the code grows exponentially. klee addresses this by employing configurable heuristics as to which branch(es) it explores first
- the "environment" problem: how shall the symbolic executor model input from the ambient execution environemnt? If the program under test, for instance, calls
fread: how shall the symbolic execution engine model that? That's a subject for a later post.
Klee has shown real-world results: they validated the GNU coreutils & found three bugs which had been present for over fifteen years.
So I Was Doing Some L33t Coding…
I recently changed jobs. I wanted a job that involved coding, which meant coding interviews (which I loathe) & that meant l33t coding (which I loathe even more). Here's a test question from "Cracking the Coding Interview" along with my initial solution:
// Cracking the Coding Interview problem 11.1 // Given two sorted arrays A & B, assume A has enough buffer at its end to // store B, merge B into A (in sorted order). // nA & nB are the sizes of A & B, resp. lastA points one-past-the end // of A's contents: // 0 1 lastA - 1 lastA nA - 1 // | A_0 A_1 ... A_{lastA-1} * ... * | void merge(int *A, int nA, int lastA, int *B, int nB) { int a = lastA - 1, b = nB - 1, ins = nA - 1; // insert at `ins` while (ins > -1) { if (A[a] > B[b]) { A[ins--] = A[a--]; } else { A[ins--] = B[b--]; } } }
My scheme was to walk \(\mathcal{A}\) backward while comparing the last un-copied elements of \(\mathcal{A}\) & \(\mathcal{B}\), copying the greater element in each comparison into place:
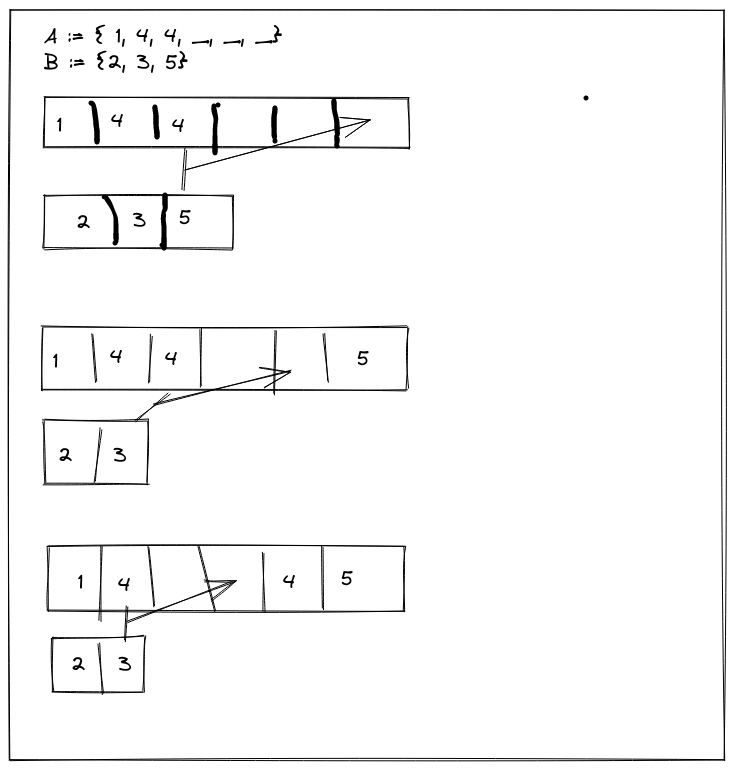
Cool, right? Tight & elegant. Employers will be drooling over me!
But.. is it right? Really right? Interviewers love to probe for corner cases, after all. Let's put klee on it.
klee only operates on a complete program, so we'll need to build up a test harness:
#include <klee/klee.h> #include <stdlib.h> // Cracking the Coding Interview problem 11.1 // Given two sorted arrays A & B, assume A has enough buffer at its end to // store B, merge B into A (in sorted order). // nA & nB are the sizes of A & B, resp. lastA points one-past-the end // of A's contents: // 0 1 lastA - 1 lastA nA - 1 // | A_0 A_1 ... A_{lastA-1} * ... * | void merge(int *A, int nA, int lastA, int *B, int nB) { int a = lastA - 1, b = nB - 1, ins = nA - 1; // insert at `ins` while (ins > -1) { if (A[a] > B[b]) { A[ins--] = A[a--]; } else { A[ins--] = B[b--]; } } } int main(int argc, char *argv[]) { int nA = 16, lastA = 8, nB = 8; int *A = (int*) malloc(nA*sizeof(int)); int *B = (int*) malloc(nB*sizeof(int)); klee_make_symbolic(A, nA*sizeof(int), "A"); klee_make_symbolic(B, nB*sizeof(int), "B"); for (int i = 0; i < 7; ++i) { klee_assume(A[i] <= A[i+1]); klee_assume(B[i] <= B[i+1]); } merge(A, nA, lastA, B, nB); for (int i = 0; i < 15; ++i) { klee_assert(A[i] <= A[i+1]); } free(A); free(B); return 0; }
By default, klee will treat our variables as "concrete"; i.e. they hold specific values, like 11, or "Hello, world!". klee_make_symbolic tells klee to treat its argument as, well, symbolic. Instead of holding a particular value like 11, klee will begin writing-down things like "a 32-bit int which is known to be > 3". Here, I'm making \(\mathcal{A}\) & \(\mathcal{B}\) be arrays of length 16 & 8 respectively, but allowing their contents to be any integers at all.
Next, I setup the preconditions via klee_assume. klee_assume lets
us tell klee things it should assume to be true. In this case, I'm
telling klee to assume that \(\mathcal{B}\) is sorted along with the
first eight elements of \(\mathcal{A}\).
Next I call merge and tell klee to prove that the final value of \(\mathcal{A}\) is sorted.
OK– let's fire this up. I put all this code into merge-1.c & compiled to bitcode:
clang-9 -I /opt/klees/current/include -emit-llvm -c -g -O0 -Xclang -disable-O0-optnone -o merge-1.bc merge-1.c merge-1.c:18:5: warning: implicit declaration of function '__assert_fail' is invalid in C99 [-Wimplicit-function-declaration] klee_assert(a >= 0 && a < nA); ^ /opt/klees/current/include/klee/klee.h:96:6: note: expanded from macro 'klee_assert' ... a few warnings
& then ran klee against that:
ls merge-1.bc merge-1.c time klee --libc=uclibc --posix-runtime --only-output-states-covering-new --optimize merge-1.bc KLEE: NOTE: Using POSIX model: KLEE: NOTE: Using klee-uclibc : KLEE: output directory is ".../klee-out-0" KLEE: Using STP solver backend KLEE: WARNING: executable has module level assembly (ignoring) KLEE: WARNING ONCE: calling external: syscall(16, 0, 21505, 93879719616896) at runtime/POSIX/fd.c:1007 10 KLEE: WARNING ONCE: Alignment of memory from call "malloc" is not modelled. Using alignment of 8. KLEE: ERROR: merge-1.c:18: memory error: out of bound pointer KLEE: NOTE: now ignoring this error at this location KLEE: ERROR: merge-1.c:18: memory error: out of bound pointer KLEE: NOTE: now ignoring this error at this location KLEE: done: total instructions = 836510 KLEE: done: completed paths = 0 KLEE: done: partially completed paths = 12870 KLEE: done: generated tests = 2 183.82user 87.06system 4:31.76elapsed 99%CPU
Huh… looks like we may have a problem. klee found two execution paths leading to out-of-bounds errors, and left the output in a sub-directory named klee-out-0. In general, klee will place output files in a sub-directory named klee-N where \(N\) is 0,1,2…:
ls -Alh total ... lrwxrwxrwx 1 mgh users 64 Aug 11 07:17 klee-last -> .../klee-out-0 drwxr-xr-x 2 mgh users 4.0K Aug 11 07:21 klee-out-0 -rw-r--r-- 1 mgh users 12K Aug 11 07:15 merge-1.bc -rw-r--r-- 1 mgh users 2.1K Aug 7 07:19 merge-1.c sp1ff: ls -Alh klee-last/ total 2.0M -rw-r--r-- 1 mgh users 1.8M Aug 11 07:17 assembly.ll -rw-r--r-- 1 mgh users 776 Aug 11 07:21 info -rw-r--r-- 1 mgh users 257 Aug 11 07:17 messages.txt -rw-r--r-- 1 mgh users 159K Aug 11 07:21 run.istats -rw-r--r-- 1 mgh users 28K Aug 11 07:21 run.stats -rw-r--r-- 1 mgh users 476 Aug 11 07:17 test000001.ptr.err -rw-r--r-- 1 mgh users 1.2K Aug 11 07:17 test000001.kquery -rw-r--r-- 1 mgh users 178 Aug 11 07:17 test000001.ktest -rw-r--r-- 1 mgh users 478 Aug 11 07:17 test000002.ptr.err -rw-r--r-- 1 mgh users 1.3K Aug 11 07:17 test000002.kquery -rw-r--r-- 1 mgh users 178 Aug 11 07:17 test000002.ktest -rw-r--r-- 1 mgh users 267 Aug 11 07:17 warnings.txt
Okay… let's have a look at the first error:
bat klee-last/test000001.ptr.err
───────┬───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ File: klee-out-4/test000001.ptr.err
───────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
1 │ Error: memory error: out of bound pointer
2 │ File: merge-1.c
3 │ Line: 20
4 │ assembly.ll line: 4003
5 │ State: 1
6 │ Stack:
7 │ #000004003 in merge (=94489744893312, =94489772997344) at merge-1.c:20
8 │ #100004166 in __klee_posix_wrapped_main () at merge-1.c:47
9 │ #200002347 in __user_main (=1, =94489744554496, =94489744554512) at runtime/POSIX/klee_init_env.c:245
10 │ #300000440 in __uClibc_main (=1, =94489744554496) at libc/misc/internals/__uClibc_main.c:401
11 │ #400000606 in main (=1, =94489744554496)
12 │ Info:
13 │ address: 94489744893308
14 │ next: object at 94489743961088 of size 58
15 │ MO17[58] allocated at main(): tail call fastcc void @__uClibc_main(i32 %0, i8** %1)
───────┴───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Line 20 is where we compare the "next" elements of \(\mathcal{A}\) & \(\mathcal{B}\):
void merge(int *A, int nA, int lastA, int *B, int nB) { int a = lastA - 1, b = nB - 1, ins = nA - 1; // insert at `ins` while (ins > -1) { if (A[a] > B[b]) { <== line 20!
… but what happened? Was the error with \(a\) or \(b\)? And was it too high or too low? And why?
klee not only detected that we had an out-of-bounds error, it produced a test case for us. Unlike the "err" file, it's not plain text; it needs to be read by a dedicated program, ktest-tool:
ktest-tool klee-last/test000001.ktest ktest file : 'klee-last/test000001.ktest' args : ['merge-1.bc'] num objects: 3 object 0: name: 'model_version' object 0: size: 4 object 0: data: b'\x01\x00\x00\x00' object 0: hex : 0x01000000 object 0: int : 1 object 0: uint: 1 object 0: text: .... object 1: name: 'A' object 1: size: 64 object 1: data: b'\x00\x00\x00\x01\x00\x00\x00\x01\x00\x00\x00\x01\x00\x00\x00\x01\x00\x00\x00\x01\x00\x00\x00\x01\x00\x00\x00\x01\x00\x00\x00\x01\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff' object 1: hex : 0x0000000100000001000000010000000100000001000000010000000100000001ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff object 1: text: ................................................................ object 2: name: 'B' object 2: size: 32 object 2: data: b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00' object 2: hex : 0x0000000000000000000000000000000000000000000000000000000000000000 object 2: text: ................................
There are \(\mathcal{A}\) & \(\mathcal{B}\): they are 64 & 32 bytes in size, respectively, but if we interpret their contents as 32-bit signed integers, they are:
\begin{equation} \mathcal{A} := [16777216, 16777216, ..(5)., 16777216, -1, -1, ..(5)., -1] \\ \mathcal{B} := [0, 0, 0, ..(5).] \end{equation}
Every element of \(\mathcal{A}\) is larger than every element of \(\mathcal{B}\). Meaning that we'll always take the "if" branch in merge, copying \(\mathcal{A}[a]\) to the next insertion point and decrementing \(a\). Oh… meaning that when we finish copying the elements of \(\mathcal{A}\) into place, \(a\) will be -1, and on the next iteration of our loop, when we should start copying the elements of \(\mathcal{B}\) into place, we'll check \(\mathcal{A}[-1]\):
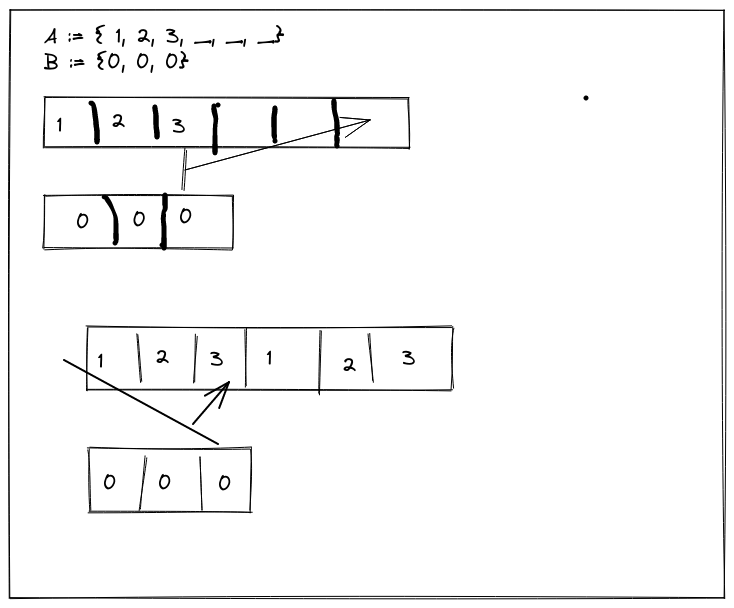
OK, well, I can fix that. What about the other case? When every element of \(\mathcal{B}\) is greater than every element of \(\mathcal{A}\)? That should be fine: we'll take the "else" on ever iteration of our loop, copy the elements of \(\mathcal{B}\) into place… and be done, so long as we terminate early enough to avoid evaluating \(\mathcal{B}[-1]\):
void merge(int *A, int nA, int lastA, int *B, int nB) { int a = lastA - 1, b = nB - 1, ins = nA - 1; // insert at `ins` while (ins > -1 && a > -1 && b > -1) { if (A[a] > B[b]) { A[ins--] = A[a--]; } else { A[ins--] = B[b--]; } } if (a < 0) { // all of A was greater than all of B-- copy B into A while (ins > -1) { A[ins--] = B[b--]; } } /* else if (b < 0) { // all of B was greater than all of A-- done } */ }
Re-compile & re-test:
clang-9 -I /opt/klees/current/include -emit-llvm -c -g -O0 -Xclang -disable-O0-optnone -o merge-2.bc merge-2.c merge-2.c:19:7: warning: implicit declaration of function '__assert_fail' is invalid in C99 [-Wimplicit-function-declaration] klee_assert(ins >= 0 && ins < nA); ^ /opt/klees/current/include/klee/klee.h:96:6: note: expanded from macro 'klee_assert' : __assert_fail (#expr, __FILE__, __LINE__, __PRETTY_FUNCTION__)) \ ^ ... some warnings time klee --libc=uclibc --posix-runtime --only-output-states-covering-new --optimize merge-2.bc KLEE: NOTE: Using POSIX model: ... KLEE: NOTE: Using klee-uclibc : ... KLEE: output directory is ".../klee-out-1" KLEE: Using STP solver backend KLEE: WARNING: executable has module level assembly (ignoring) KLEE: WARNING ONCE: calling external: syscall(16, 0, 21505, 94249972569680) at runtime/POSIX/fd.c:1007 10 KLEE: WARNING ONCE: Alignment of memory from call "malloc" is not modelled. Using alignment of 8. KLEE: done: total instructions = 3127359 KLEE: done: completed paths = 12870 KLEE: done: partially completed paths = 0 KLEE: done: generated tests = 3 1138.67user 2054.16system 53:21.29elapsed 99%CPU
This execution took considerably longer (almost 20 minutes), but completed with no errors detected & three test cases:
\begin{equation} \mathcal{A} := [0, 0, 0, 0, 0, 0, 0, 0, -1, -1, -1, -1, -1, -1, -1, -1] \\ \mathcal{B} := [0, 0, 0, 0, 0, 0, 0, 0] \end{equation}In this case, we'll take the "else" branch in "merge" every time, until \(b\) becomes -1, at which point we're done.
\begin{equation} \mathcal{A} := [16777216, 16777216, ..(5)., 16777216, -1, -1, ...] \\ \mathcal{B} := [0, 0, 0, 0, 0, 0, 0, 0] \end{equation}This was the case that tripped me up in my first implementation: we'll take the "if" branch every time until \(a\) is -1, and then copy \(\mathcal{B}\) into place in the "tidy-up" loop at the bottom.
\begin{equation} \mathcal{A} := [1, 1, 1, 1, 1, 1, 1, 2, -1, -1, -1, -1, -1, -1, -1, -1] \\ \mathcal{B} := [0, 0, 0, 0, 0, 0, 0, 1] \end{equation}This is the most interesting case: we'll take both arms of the if-then-else construct, and hit the "tidy-up" loop at the bottom.
Given the variation in control paths, I'd say the three cases klee selected would make a very reasonable start to a unit test suite.
Where are we?
At this point, I've proven my algorithm works for all arrays where \(|\mathcal{A}| = 16\) and \(|\mathcal{B}| = 8\). That's not complete, but it inspires confidence.
Klee can be a bit intrusive. You have to compile your code specially (i.e. to bitcode) as well as carrying out your native build process. If your program links to other libraries, you need to compile them to bitcode as well in order to get true symbolic execution when your code calls into those libraries.
It can also be slow: unearthing my bug took about three minutes. Three minutes to run a test suite is fine, in my opinion– you can get a cup of coffee. Showing that there were none left for my limited case took twenty. Twenty minutes is a problem: you're going to context-switch. I went ahead and made the array sizes symbolic as well (with max sizes of 16 & 12) and let it run for twelve hours– it never terminated. Alright it's a big problem, but klee appeared not to take advantage of the resources available to it: I kept an eye on htop while it was running, it never came close to taking up the 32Gb of RAM I gave it, and it never seemed to take up anything more than one core, even though it had thirty-two available.
On the other hand, one could argue that it was a silly question to ask of klee. Randomly trying different sizes could work, but only up to some limit, and seems like a blunt instrument in any event. I'd like to use klee to prove something like "merge is correct for \(|\mathcal{A}| = n\) and all \(\mathcal{B}\) where \(|\mathcal{B}| < n\)", for some small value of \(n\), and then prove "assuming that, show merge is correct for \(n+1\)". At this point, however, I think we're out of the realm of symbolic execution (and into that of automated theorem provers?)
I'm going to be trying some other tools (haybale, Crux, and angr are on my list) on this, as well as putting them all on some other test problems. My goal is to build a toolkit of some kind that the working coder could use like a unit test suite: but instead of writing a unit test for a new function, they could prove statements about their new function. Just as starting with your unit test leads to "test-driven develeopment", I'm curious as to what "reasonability-driven development" would look like.
08/12/21 07:26